Slope-Intercept Form: Definition, Formula, and Calculations

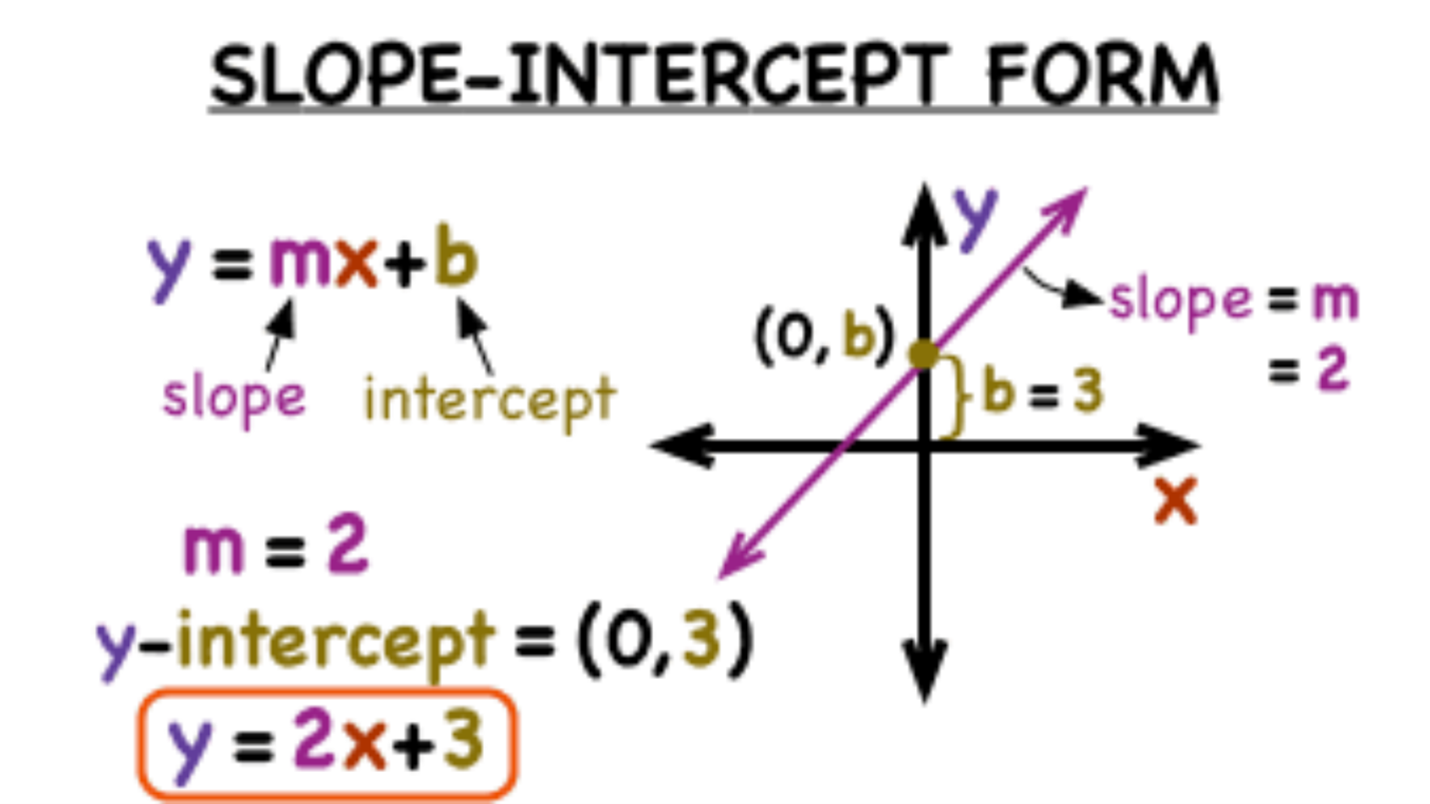
The slope-intercept form is a significant subject matter in the study of linear equations especially working with the equation of straight line, which is the core dimension, used in algebraic expressions.

Slope compute the steepness or inclination of line and Intercept point out the position in coordinate system where line touches a coordinate axis. The slope intercept form is very useful to work out with the problems involving lines and graphs.

It describes the linear relationship b/w the variables (independent and dependent) to estimate the rate of change. In this article we will elaborate slope-intercept from, it’s definition, formula and at last we will solve some examples.

Definition of Slope-Intercept Form:

The slope-intercept form is a technique used to find out the equation of straight line. To compute equation of straight line, we need some information about the slope (which is also termed as Gradient sometimes), a point where the line touches y-axis.

Before going to introduce its formula, it is necessary to note that a rectangular or Cartesian plane comprises of two straight lines bisecting each other at an angle of 90⁰ and their point of intersection is called origin denoted 0.

One is horizontal line known as x-axis and second is vertical line known as y-axis respectively.

Formula:

Mathematically, the slope-intercept form can be defined as

y = mx + c

In the above equation,

• y is the dependent variable
• m is the slope of the line
• x is an autonomous (independent) variable
• c is y-intercept (A point where line touches y-axis)

Where,

Slope = m = 𝚫y/ 𝚫x = (y₂ – y₁)/ (x₂ – x₁)

We can also comprehend that slope is rise (change along vertical axis) over run (change along x-axis). Some important facts about slope of a line are given below:

• Gradient will be 0, if the straight line is horizontal i.e. parallel to x-axis.
• Gradient will be undefined, if the straight line is vertical i.e. parallel to y-axix.
• Gradient is positive if 𝚫y and 𝚫x have the same signs.
• Gradient is negative if 𝚫y and 𝚫x have opposite signs.
• If m > 0, it implies both variables x and y are directly proportional to each other.
• If m < 0, then both variables x and y are inversely proportional to each other.
• If c > 0, then y-intercept will be above the origin on y-axis.
• If c < 0, then y-intercept will be below the origin on y-axis.

Calculations of Slope Intercept Form

Since we have already elaborated here that slope-intercept form is used to compute the equation of straight line. Now we will discuss here some useful techniques to find the equation of straight line using the concept of slope-intercept form explaining some cases with the help of examples.

• When gradient and y-intercept are given
• When two pints are given
• When gradient and one point are given

A y=mx+b calculator can be used to find the slope intercept form according to the above cases with a step-by-step solution. Below is a manual method to find the slope intercept form according to the given cases.

Case 1. When gradient and y-intercept are given

Example 1.

Compute the equation of straight line if gradient is 2 and y-intercept is 4.

Solution:

Step i. Write down the given data.

m = 2, c = 4

Step ii. Use slope-intercept formula to find out equation of straight line.

y = mx + c

Step iii. Place the relevant values in the above formula and simplify.

y = (2)x + (4) = 2x + 4 Ans.

Example 2.

Calculate the equation of straight line if gradient is -3 and y-intercept is 1.

Solution:

Step i. Write down the given data.

m = -3, c = 1

Step ii. Write down slope-intercept formula.

y = mx + c

Step iii. Place the relevant values in the formula and simplify.

y = (-3)x + (1) = -3x + 1 Ans.

Case 2. When two points are given

Example 1.

Determine the equation of straight line using slope-intercept form from the points (4, 2), (8, 6)

Solution:

Step i. Write down the given data.

x₁ = 4, x₂ = 8, y₁ = 2 and y₂ = 6

Step ii.  Evaluate slope of the line.

m =  𝚫y/ 𝚫x = (y₂ – y₁)/ (x₂ – x₁)

m = (6 – 2)/ (8 – 4)

m = 4/ 4

m = 1

Step iii. Compute the value of c i.e. y-intercept using the value of gradient and any one point in slope-intercept formula.

y = mx + c

2 = (1) (4) + c             [using (2, 3)]

2 = 4 + c

2– 4 = c

c = 2

Step iv. Place the values of m and c in slope-intercept formula.

y = mx + c

y = (1)x + 2

y = x + 2 Ans.

Case 3. When gradient and one point are given.

Example 1.

Determine the equation of straight line if m = 2 and point is (1, 1).

Solution:

Step i. Write down the given data.

Here m = 2, x = 1 and y = 1

Step ii. Compute the value of c i.e. y-intercept using the given point and the value of gradient in slope-intercept formula.

y = mx + c

1 = (2) (1) + c

1 = 2 + c

1 – 2 = c

c = -1

Step iii. Place the values of m and c in slope-intercept formula.

y = mx + c

y = (2)x + (-1)

y = 2x – 1 Ans.

Example 2.

Determine the equation of straight line if m = 1 and point is (1, 2)

Solution:

Step i. Write down the given data.

Here m = 1, x= 1 and y = 2

Step ii. Compute the value of c i.e. y-intercept using the given point and the value of gradient in slope-intercept formula.

Y = mx + c

2 = (1) (1) + c

2 = 1 + c

2 – 1 = c

c = 1

Step iii. Place the values of m and c in slope-intercept formula.

y = mx + c

y = (1)x + 1

y = x + 1 Ans.

Summary:

In this article we talked about slope-intercept form which is the core dimension of equation of the straight line. We introduced its formula and briefed all its concerning terminologies as well as we discussed the cases to determine the equation of straight line with the help of examples.