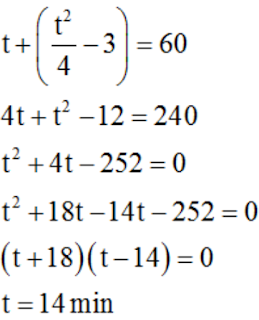CBSE Class 10th Maths Important MCQs from Chapter 4 Quadratic Equations with Solutions 2023-24
Get here more Important MCQs for Class 10 Maths Chapter 4 - Quadratic Equations to help in the preparation for the Board Exam 2023-2024.
1. The roots of quadratic equation 5x2 – 4x + 5 = 0 are
(A) Real & Equal
(B) Real & Unequal
(C) Not real
(D) Non-real and equal
Answer: (C)
Explanation: To find the nature, let us calculate b2 – 4ac
b2 – 4ac = 42 – 4 x 5 x 5
= 16 – 100
= -84 < 0
2. Equation (x+1)2 – x2 = 0 has _____ real root(s).
(A) 1
(B) 2
(C) 3
(D) 4
Answer: (A)
Explanation:
Since (x + 1)2 – x2 = 0
⟹ x2 + 1 + 2x – x2 = 0
⟹ 1 + 2x = 0
⟹ x= -1/2
This gives only 1 real value of x.
3. Which constant should be added and subtracted to solve the quadratic equation 4x2 − √3x + 5 = 0 by the method of completing the square?
(A) 9/16
(B) 3/16
(C) 3/4
(D) √3/4
Answer: (B)
Explanation:
This can be written as
Hence the given equation can be solved by adding and subtracting 3/16.
4. If 1/2 is a root of the equation x2 + kx – (5/4) = 0 then the value of k is
(A) 2
(B) – 2
(C) 3
(D) –3
Answer: (A)
Explanation:
As one root of the equation x2 + kx – (5/4) = 0 is 1/2
5. A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.
(A) 3
(B) 8
(C) 4
(D) 7
Answer: (B)
Explanation:
Let the number be x
Then according question,
x + 12 = 160/x
x2 + 12x – 160 = 0
x2 + 20x – 8x – 160 = 0
(x + 20) (x – 8) = 0
x = -20, 8
Since the number is natural, so we consider only positive value.
6. The product of two successive integral multiples of 5 is 300. Then the numbers are:
(A) 25, 30
(B) 10, 15
(C) 30, 35
(D) 15, 20
Answer: (D)
Explanation:
Let the consecutive integral multiple be 5n and 5(n + 1) where n is a positive integer.
According to the question:
5n × 5(n + 1) = 300
⇒ n2 + n – 12 = 0
⇒ (n – 3) (n + 4) = 0
⇒ n = 3 and n = – 4.
As n is a positive natural number so n = – 4 will be discarded.
Therefore the numbers are 15 and 20.
(A) 3.5
(B) 4
(C) 3
(D) – 3
Answer: (C)
Explanation:
Since y cannot be negative as negative square root is not real so y = 3.
8. If p2x2 – q2 = 0, then x =?
(A) ± q/p
(B) ±p/q
(C) p
(D) q
Answer:(A)
Explanation:
p2x2 – q2 = 0
⇒p2x2 = q2
⇒x = ±p/q
(A) 3
(B)5
(C) 4
(D) 7
Answer:(B)
Explanation:
10. If x2 (a2 + b2) + 2x (ac + bd) + c2 +d2 = 0 has no real roots, then
(A) ad≠bc
(B) ad<bc
(C) ad>bc
(D) all of these
Answer: (D)
Explanation:
If equation has no real roots then discriminant of the equation must be less than zero.
11. If the one root of the equation 4x2 – 2x + p – 4 = 0 be the reciprocal of other. Then value of p is
(A) 8
(B) – 8
(C) – 4
(D) 4
Answer: A
Explanation:
If one root is reciprocal of other, then product of roots is:
12. Rohini had scored 10 more marks in her mathematics test out of 30 marks, 9 times these marks would have been the square of her actual marks. How many marks did she get in the test?
(A) 14
(B) 16
(C) 15
(D) 18
Answer: (C)
Explanation:
Let her actual marks be x
Therefore,
9 (x + 10) = x2
⇒x2 – 9x – 90 = 0
⇒x2 – 15x + 6x – 90 = 0
⇒x(x – 15) + 6 (x – 15) = 0
⇒(x + 6) (x – 15) = 0
Therefore x = – 6 or x =15
Since x is the marks obtained, x ≠ – 6. Therefore, x = 15.
13. A train travels at a certain average speed for a distance of 63 km and then travels a distance of 72 km at an average speed of 6 km/h more than its original speed. If it takes 3 hours to complete the total journey, what is its original average speed?
(A) 42 km/hr
(B) 44 km/hr
(C) 46 km/hr
(D) 48 km/hr
Answer: (A)
Explanation:
Let the original speed be x,
Then according to question
This gives x = -3 and x = 42
Since speed cannot be negative, so we ignore –3,
Therefore original average speed is 42 km/hr.
14. Satvik observed that in a clock, the time needed by the minute hand of a clock to show 3 PM was found to be 3 min less than t2/4 minutes at t minutes past 2 PM. Then t is equal to
(a) 14
(b) 15
(c) 16
(d) None of these
Answer: (A)
Explanation: We know that the time between 2 PM to 3 PM = 1 hr = 60 min
Given that at t minutes past 2 PM, the time needed by the minute’s hand of a clock to show 3 PM was found to be 3 minutes less than t2/4minutes
Therefore,
15. A takes 6 days less than B to finish a piece of work. If both A and B together can finish the work in 4 days, find the time taken by B to finish the work.
(A)12 days
(B) 12 ½ Days
(C) 13 days
(D) 15days
Answer: (A)
Explanation: Let B alone finish the work in x days.
Therefore, A alone can finish the work in (x – 6) days
A’s one day work = 1/x-6
B’s one day work = 1/x
Given that (A + B) can finish the work in 4 days.
Therefore, A’s one day work + B’s one day work = (A + B)’s one day work
As, x ≠ 2 , because if x = 2 , then A alone can finish work in (2 – 6) = – 4 days which is not possible.
Therefore we consider x = 12.
This implies B alone can finish work in 12 days and A alone will finish the work in 12 – 6 = 6 days.